The Haversine Formula

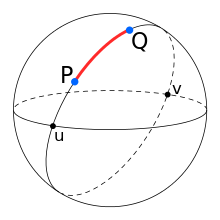
To travel the shortest distance between any two points on the surface of a sphere you need imagine a circle passing through both of those points which has its centre at the same point as the sphere and travel along its route. We call these loops great circles.

A Great Circle

Being able to work out the length of the arc of a great circle given the latitude and longitude of each location was an important problem in navigation. There are several ways to resolve the problem, but what an ideal solution would have was succinct form that didn't require too many tables to look up during the process. By using trig functions other than the ones that perhaps you are used to we can do it using just cos and one other function, namely haversin. Below is a wonderful diagram showing many of the more obscure trig ratios. The one to pay attention to for this article is versin (green): 

The unit circle demonstrating some of the less common trig ratios. It is interesting to note csc, sec and cot which we don't usually think about as anything tangible.

Versin (literally, re(ver)se sine) is 1-cos(theta) is the bit that you add onto cosine to get the radius of the circle. Haversin (literally (Ha)lf re(ver)se sine) is just half of that. This leads to the relatively nice formula below:

The haversin formula

Where d is the distance we are trying to find, r is the radius of the Earth and each point has latitude and longitude (λ(i),ϕ(i)) in radians.

The Earth isn't perfectly spherical, see here for more details on this, but this formula holds true within 0.5% so it endured a long shelf life in terms of pre computing navigation mathematics. All you required was a table of pre worked out values of cos and haversin, which became standard.