The Chain Puzzle

This puzzle outdates even Dudeney being the masterpiece of the puzzelist Sam Lloyd. However, I will quote Dudeney’s phrasing because I always find them amusing and it helps me fuel the fantasy in my head that the Victorian times were full of eccentrics doing puzzles rather than the reality of a racist, sexist, workhouse filled time where they spent their time destroying all architectue older than them. Anyway:

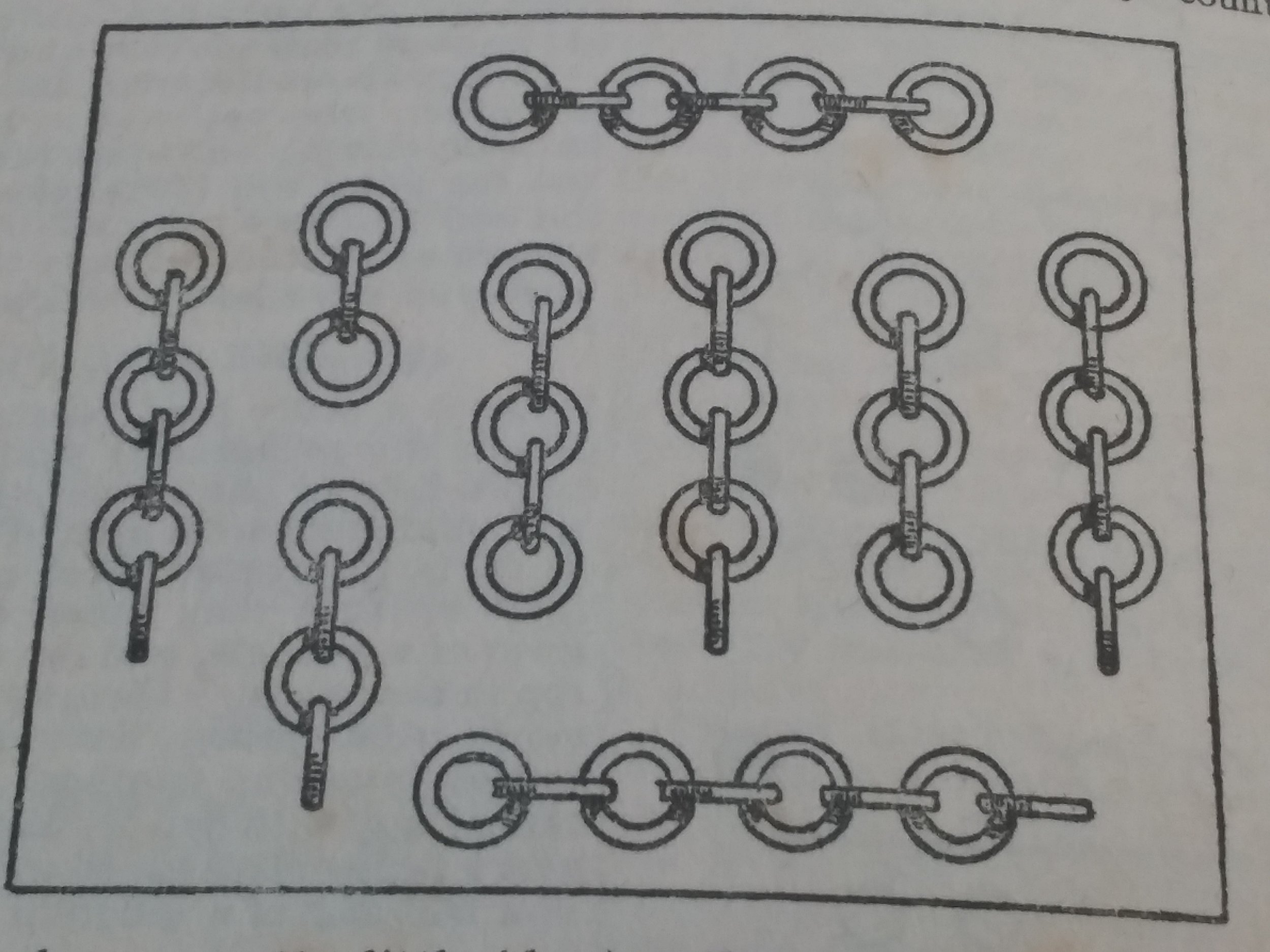
“A man had nine pieces of chain, as shown in the illustration. He wanted to join these fifty links into one endless chain. It will cost a penny to open any link and twopence [pronounced tuppunce] to weld a link together again, but he could buy a new endless chain of the same character and quality for 2s. 2d. [2 shillings and 2 pence. One shilling is worth 12 pence.] What was the cheapest course for him to adopt? Unless the reader is cunning he [xe, sigh] may find himself [xeirself] a good way out in his [xeir] answer.

Answer below:

…

There are 9 lengths of chain, so going brute force and opening then sealing one ring from each gives 9×(2+1)=27=2 shillings and threepence [pronounced thrup-unce] which means it would be cheaper to buy a new chain. However, by taking all of the rings which are used for sealing from few chains we can do better. By splitting up the length of 8 and then using those 8 rings to seal up the remaining 8 chains we can get by with 8×(2+1)=24=2 shillings exactly. When I first saw this puzzle a few years ago I got to this answer and assumed I had finished. But in fact we can go slightly better. With this knowledge can you find an improvement? Answer below:

…

Instead of breaking up the length of 8, let’s break up the length of 3 and the length of 4. This gives a total of 7 rings for sealing purposes and there will be 7 lengths left to seal. Thus we can repair the chain with 7×(2+1)=21=1 shilling 9 pence. This is optimal.