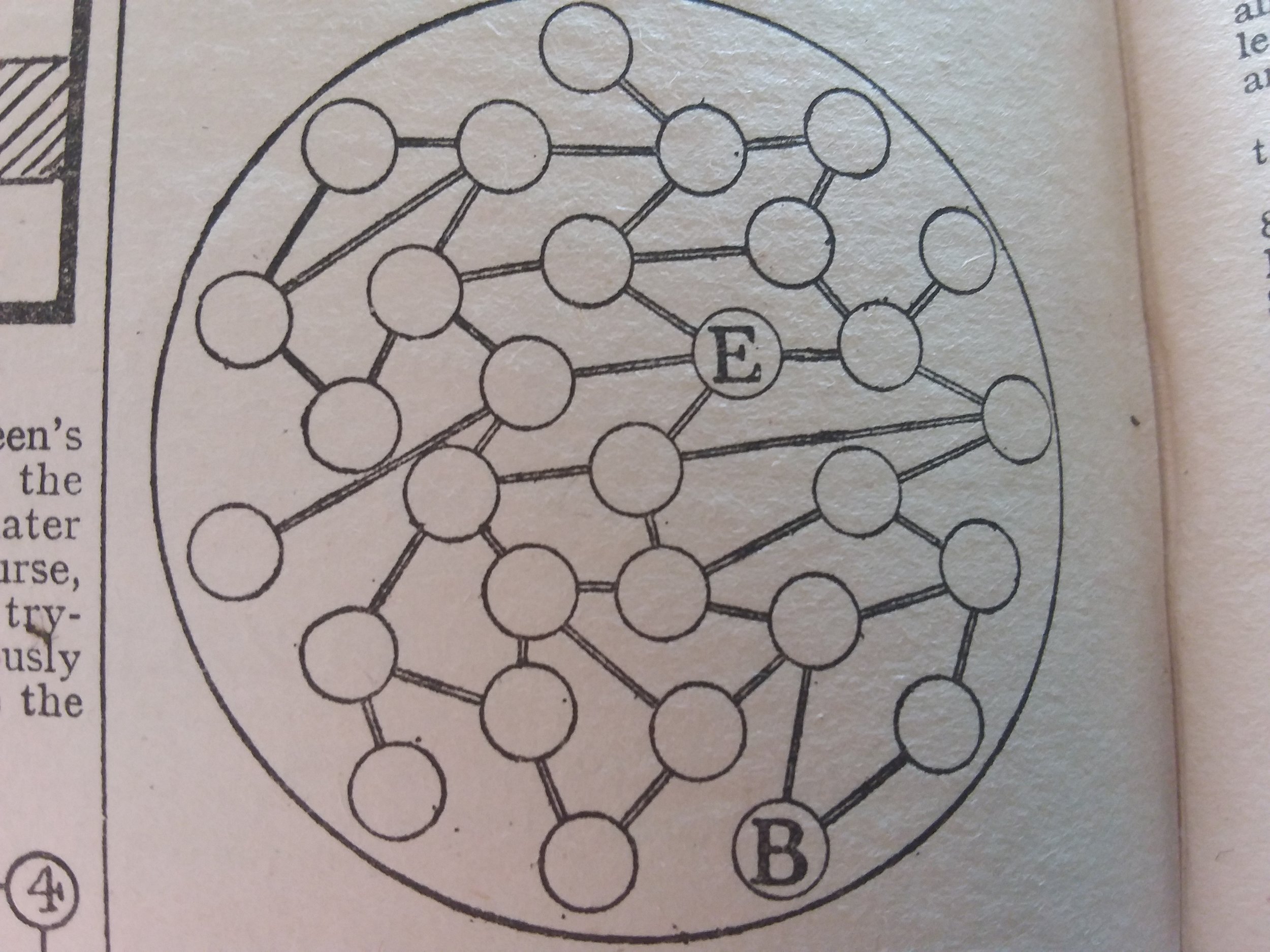
The Wargame Problem

Sometimes puzzles cross the line and act more like small games. In the wargame there are two players moving tokens around a map. The token marked B (for British. If you regularly read this website then you know exactly where I got this one from) is attempting to capture the othe token and it is B that moves first.

Each move travels to one of the connected circles and staying still is not an option. Can the other token stay alive forever?

Feel free to try it yourself, but I'm going to move straight on to the analysis because it illustrates a neat idea thatwe've used before on this website, that of parity. For more examples of the use of parity in proofs see Tetris Lights (video) and this similar tetramino laying problem (text).

Have a look at the colouring below. On B’s first turn they must move to a red square, then E must also move to a red square. For their second moves the opposite is true with both of them moving onto blue squares. So, at the start of B’s move each turn they will always be on the same colour square as E, but they will always have to go on to the other colour; thus they can't capture E. They are in phase with each other.

However, I have omitted the colour from the top left corner. It is only in that corner where you can't alternate the colour scheme of red and blue. By going around this loop you manage to end up on the opposite colour than you should have been and so you can put yourself out of phase.

As long as you make sure that your opponent doesn't also take a trip around the loop, you should now capturing the other token trivial; just head towards them. With best play it shouldn't take more than 17 moves to win of which the first 9 are heading around the loop.