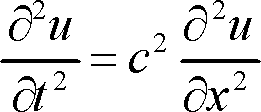Pretty Maths

A few days ago I was doing some maths marking on the train home from work and a stranger asked a request of me. He said he could see that I knew something about maths and he was training to design prints for textiles and his particular project at the moment was to try and make a print out of equations. In the past he had found some to use, but on closer inspection (and a bit of googling) he realised they were meaningless. What he wanted was equations which were both visually interesting and factually true. I can sympathise: the further you get in mathematics the more you realise that set designers for films often don't know what they are doing when they try to write "maths" on the whiteboards behind characters in a school setting.

As someone who designed some maths shoes I was probably quite a good person to ask and so last night I drew out some equations which I chose to meet several criteria. Firstly they must be correct, but more than that I wanted them to be individually profound. Secondly I wanted them to be visually beautiful even if you didn't understand them at all, so lots of greek letters. Thirdly they had to be coherent together; nothing screams incorrect maths like seeing unrelated maths posted next to each other. Seeing the differential equations, topology and group theory all mixed up looks messy (although, I suppose it could all be used together on some problems).

This is what I came up with, all taken from university level applied maths with a big physics theme:

Left hand side

I'll do a quick run down why I picked each of these and then show the second half below.

Maxwell's equations are differential equations that link electronic waves with magnetic waves (they are very related concepts). Each variable has both its divergence and its curl (written with the triangles and either a dot or a chevron) so they form a visual symmetry. The rest of the letters are just constants that link to physical things.

Euler's equation has to make any list of beautiful maths, but I feel like a sell out by putting it. Still it is linked to most of the other equations on the page so it earns its place.

The fundamental theorem of calculus highlights that doing the anti derivative of a function and finding the area under a function are the same thing. This is not at all obvious hence the grand name. Also I wanted an integral symbol, they are weird while still being recognisable as mathsy by the general public (I think) and they are just kind of pretty.

Hamilton's Quartonion equation was the grounding of an extension of numbers past the imaginairies. When the idea popped into Hamilton's head he immediately carved them into the brickwork on the bridge he was walking over. The idea is that we can have 3 separate square roots of negative one and we can still get a consistent mathematics. But more than that the equation has some nice symmetries to it, so it passed the threshold for beauty.

Right hand side

Starting at the top again we have the wave equation. It together with the heat equation (6th down) are classic 2nd order differential equations and both produce satisfying solutions sets with interesting applications for physical phenomena. The curly deltas were pretty.

Next I  included the definition of differentiation because it had the limit sign in it.

One of the forms of Navier Stokes equation from fluid dynamics. I looked through my university notes to get the version with the nicest appearance and I settled on this one because it was a glorious mess of a bit of every symbol and alphabet.

E=mc^2 is for peasants. I prefer the version with the relativistic correction factor.

Schrodinger's Equation is what the whole of quantum mechanics is based on and it writes the formula in such a weird way that I think it is has an odd beauty to it. Again the del (triangle) and the Greek letters help its case.

Logistic growth is representing both the discrete equations and is the sole representative of biology on the page.

And finally who doesn't love a two tiered square root? This one is firmly within A Level (physics) territory, but it is still pretty.