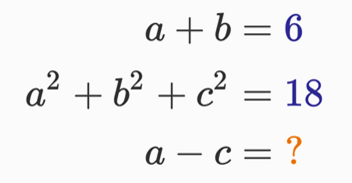Not Enough Information?

I'm not sure whether if it is just because Facebook or Google has picked up that I like maths or whether everyone gets them, but I see a lot of sudo maths go past. Usually it will have some inflammatory title like: "Only 1% of people get this right" and the question is either a system of simultaneous equations (sometimes with pictures representing the values rather than letters) or a purposefully obtuse BIDMAS question like: 4 - 3 x 5 + 1. I don't like these sort of things and yet I still find myself quickly scanning through people's answers. Clickbait is effective I guess. 

I saw one today which caught my eye in that it looked like it was actually written by a mathematician. The equations just looked right:

The person asking it stated that a, b and c were real, so I thought I'd give it a go. What struck me as interesting was that there didn't appear to be enough information. Usually to solve something with 3 unknowns we need 3 equations (and in general n unknowns needs n equations).

Using the first equation to eliminate b in the second we get:

Now we are after a quantity a - c which we might as well give a name to. Let's define a - c = k. Using this let's eliminate c to get an equation in only a and k:

We still have 2 unknowns which would normally make this unsolvable. However if we try solving this quadratic for k we get:

Notice inside the square root I completed the square and I end up for a negative discriminant (and therefore imaginary answers) except for when a = 3. So we did have a third piece information after all; the fact that the answers had to be real. Once we have a = 3 everything else pops out. The final answer was k = 3 and the individual values were a = 3, b = 3 and c = 0. All of these were unique and that was surprising. This is what I want to see my Facebook feed full of: puzzle which have some sort of aha moment in them.